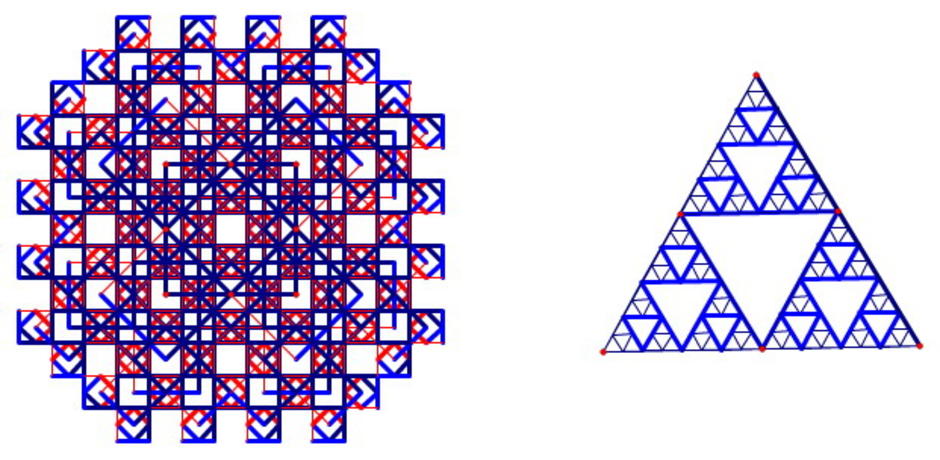
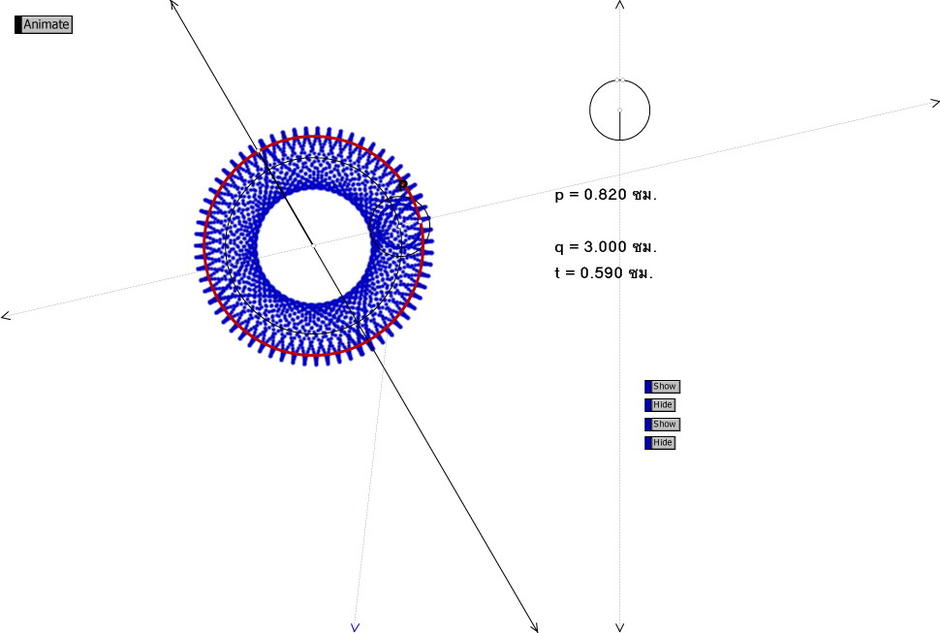
การสะท้อน The Geometer's Sketchpad
อยากฝากผลงานสวยๆ นี้ให้เพื่อนๆ ได้ลองคิดกันว่าถ้าจะทำ ผลงานตัวนี้มีวิธีการสร้างอย่างไร
ไฟล์ผลงานการสะท้อน ดาวน์โหลด เลยค่ะ
การสร้าง วิธีการสร้าง จะต้องใช้ความรู้เกี่ยวกับการสะท้อน และ การย่อขยายเข้ามาช่วย ผลงานตัวนี้จะช่วยให้เด็กนักเรียนเกิดความคิดสร้างสรรค์ มองเห็นความสวยงามของรูปทรงเรขาคณิต
นักเรียนบ่นหลายคนว่าทำตามไ่ม่ทัน ถ้าทำตามไม่ทันรูปภาพด้านบน
ก็อ่านบทความประกอบไปด้วยเลยแล้วกันนะค่ะ
เริ่มต้น นำเครื่องมือเขียนเส้นในแนวตรงออกมาสร้างมุมดังรูป และสร้างรูปต้นแบบ ห้าเหลี่ยมที่จะใช้เพื่อสะท้อนขั้นสอง เติมสีใส่ต้นแบบ และระบุเส้นสะท้อนในที่นี้ระบุเส้นสะท้่อนในแนวนอนก่อนจากนั้นสะท้อนรูปต้นแบบมา จะได้รูปสะท้อน1 และจะห็นว่ารูปที่สะท้อนมานั้นถูกปลุกให้ตื่นอยู่ จากนั้นระบุเส้นสะท้อนในแนวตั้ง สะท้อนรูปต้นแบบ1 ไปอีก ระบุเส้นสะท้อนแนวตั้งแนวนอนสลับกันไปมาจนได้รูปที่สะท้อนทั้งหมดหกรูป
ขั้นที่สาม ซ่อนรูปต้นแบบตัวแรก เหลือแค่จุดห้าจุดของรูปต้นแบบไว้ จากนั้นคลิกรูปทั้งหมดหกรูปปลุกให้ตื่นทั้งหมด ระบุจุดศูนย์กลางโดยดับเบิ้ลคลิกที่จุดที่เป็นมุม แล้วไปที่เมนูการแปลงย่อขยายเป็นอัตราส่วน -1/2
ขั้นที่สี่ ทำในทำนองเดียวกันย่อขยายรูปเขาไปอีกเป็นระดับ 3 ชั้นทั้งหมด ใส่สีสลับกันไปมาให้สวยงาม ควรเลือกสีที่เหมาะสม ถ้าเลือก สีฟ้าสีแดง เวลาสีซ้อนกันแล้วจะเกิดสีดำขึ้นมาไม่สวย ควรหลีกเลี่ยงจ้า ต้องมีศิลป์ ในการเลือกสีด้วยนะค่ะ ผลงานที่ออกมาถึงจะสวยงาม
ขั้นที่ห้า เป็นการรวมจุดกับเส้นตรงและวงกลมที่สร้างมาเพิ่มใช้ในการเคลื่อนไหว โดยวิธีการเลือก จุดทำตามรูปภาพเลยนะค่ะ เริ่มที่จุดกับแขนของมุมก่อน ตามรูป ไปที่เมนูแก้ไข และก็รวมจุดกับเส้นตรง
ขั้นตอนนี้ต้องเลือกจุดให้ดีนะค่ะไม่งั้นจะไม่เหมือนกับผลงานที่เรานำมาแสดง แต่จะกลายเป็นรูปทรงใหม่แทน ซึ่งก็แล้วแต่ คนทำเป็นคนพิจารณาแล้วกัน เพราะอาจจะคิดว่าผลงานแบบที่ตนทำก็เก๋ แปลกตาไปอีกแบบ ก็เป็นอันเสร็จสิ้นกระบวนการสร้างเรียบร้อยแล้ว คงต้องดูภาพพิจารณาตามไปด้วยนะค่ะ
จึงจะได้ในรูปแบบที่ต้อง
หวังว่าคงจะชอบและสนุกกับการสร้างผลงานในครั้งนี้นะค่ะ ขวัญว่าผลลัพธ์ไม่น่าตื่นตาตื่นใจเท่้ากับวิธีการที่เขาคิดได้อย่างไร สร้างได้อย่างไร อันนี้น่าสนใจและน่าทึ่งกว่า แล้วอย่าลืมฝึกฝนกันบ่อยๆนะค่ะ